Fermats Last Theorem

I finished reading Simon Singh's 'Fermat's Enigma' and had earlier read his 'Fermats Last Theorem ( FLT )'. I am yet to come across a problem which a ten year old can understand, appears deceptively simple and yet has been one of the toughest problems in mathematics and and took over 300 years to prove. Simon obviously makes it an interesting read, a racy thriller so to say.

This is going to be a long one. I want to talk about certain things in detail, which I liked, though I will keep it simple.


Let me start with, what is FLT and why its called so ? We all know whats Pythagoras Theorem. One of the most fundamental theorems which everyone has to learn irrespective of which stream they study. Its says for a right angled triangle, the square of the hypotenuse equals sum of the square of the two other sides. Mathematically presented


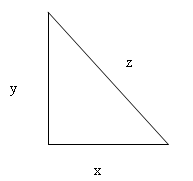
x^2 + y^2 = z^2 where

The above equation in a general form would look like


x^n + y^n = z^n [ has no whole no. solutions for n>2 ]


Fermat, born on Aug 20 ( I am Aug 19 ! ), 1601, proposed that there are no whole no solutions to the above equation for n>2 !!! and said he has the proof !! So the only form its true is the Pythagoras Equation. Fermat had studied all the theorems written in Diophantus's 'Arithmatica' and had solved them. This particular one he didn't write the proof, citing that there was not enough space. Of all his theorem's, this remain unresolved, it came to be called as FLT. He was the architect of Calculus though popularly its known more with with Newton ( even I thought so till I read this ! ).


Andrew Wiles, Professor of Mathematics at Princeton Univ proved it in 1993 after seven years of isolated laborius research ( there were certain gaps which were corrected by 1994 ). The proof takes us through the myriad journey of various forms of mathematics.


It starts with the concept of proof - and how mathematical proof differs with scientific proof. In science one can carry experiments and if results are consistent, it can taken as true. Doesn't work in mathematics. Every theorem has to be proven beyond doubt. Its built of infallible logic. It may be true for trillion observations and may be proven wrong for trillion plus one. And since most proofs incorporate other proofs, all the cards could collapse, which would be disastrous.


This theorem was attempted mainly by number theorists. These guys are always on the look for relationships. So we had whole nos to start with, moved to rational nos. to take care of fractions, then irrational nos ( most famous being pi ), invented negative nos and lastly 'imaginary' nos. These were important discoveries from the perspective of 'philosophy of completeness'. For eg. 5 - 3 = 2, but what happens if its 3 - 2 ( and this happens in debt transactions ), hence negative nos were invented/introduced. It was a similar situation for Bombelli, who was working on square root of 1. Let me use the symbol _/ for square roots.


_/1 = 1, because 1*1 = 1, but a lesser thought answer is -1, because -1*-1 = 1, as well. Moving on, so then what is the _/-1 ? Thats when imaginary nos were invented : _/-1 = i. But if there is a an i, there has to be 2i, 3i...., i/2 etc. The problem was where do they fit on the no. line and hence a vertical axis was created in the no. line. This actually solved most of the problems of mathematics.

On the way, number theorists, found some interesting relationships. One of them was the 'perfect nos' - divisors of the no. add up to the no. itself. For eg. lets take 6, divisors of 6 are 1,2 and 3, which add up to 6. So is the case with 28 ( 1,2,4,7,14 ). Check for others ? I will give you next four - 496; 8,128; 33,550,336; 8,589,869,056.

Other one being friendly nos ( again by Fermat ). They are pairs of nos such that each no. is sum of the divisors of the other no. For eg. 220 ( 1,2,4,5,10,11,20,22,44,55,110 ) and 284 ( 1,2,4,71,142 ). Couple of interesting things, I learnt on these amicable nos. Talismans in those ages inscribed these nos as they were considered to promote love. Lovers used to inscribe these on fruits and eat it as 'mathematical aphrodisiac'. I love this piece !! Some of the other pairs are 1,184 - 1,210 ; 17,296 - 18,416 ; 9,363,584 - 9,437,056.


The journey also included various methods of proving a theorem. Some of them pioneered by Euclid. In his, 'The Elements', he talks about 'Reductio ad Absurdum' ( proof by contradiction). If you want to prove a theorem to be true, start by assuming it to be false ( bizzare !! isnt it, but works ) and then go on solving it, till it reaches a point of absurdity, hence the original assumption is wrong, hence the theorem is proved to be true.


Another good one is 'Proof by Induction'. Prove it for the first piece of the equation and one ends up collapsing all the cards i.e. ends up proving for all the cases, if true for one. The most popular eg. being proof of :


Sum of 'n' nos = 1/2 *n ( n+1 ) [ you guys can check this out, if you need, write to me separately and I will send it across ]


Another piece which had a devatating effect on FLT was Godel's assertion on undecidability. He put across two theorems of undecidability; first, If axiomatic set theory is consistent, there exists theorem's that can neither be proved nor disproved !! and the second, There is no constructive procedure that will prove axiomatic theory to be consistent. This piece was generally devastating for mathematics. In simple words, it says that no matter what set of axioms are used, there would be questions which mathematics could not answer, so you will never achieve completeness ( remember I spoke about this philosophy in the earlier para ) and second one is even worst - consistency could never be proved - you meaning mathematicians can never be sure that there axioms would not lead to contradiction. Mathematicians started thinking may be FLT could never be proved.


What I liked more was the way above statements have been explained to laymen like us. Its the 'Liars Paradox' invented by Epimenides. Examine the statement said by Ajit:


' I am a Liar'


Lets see whether this statement is 'true' or 'false'. Assume its 'true'. So it implies that Ajit is a liar. But we assumed that Ajit made a true statement and therefore Ajit is not a liar. And we have an inconsistency. Lets assume that the statement is 'false'. This implies that Ajit is not a liar, but we assumed that he made a false statement, and hence Ajit is a liar - we have another inconsistency. So whether we assume the statement to be 'true' or 'false', we end up having inconsistency and therefore the statement is neither 'true' nor 'false. Hence this statement doesn't have any proof.


So lets move on to parts of mathematics which finally shaped the proof of Fermats Last Theorem. The study of elliptic curves ( equations ), modular forms and mathematics of 'symmetry' and hyperbolic space ( 4 dimensional space). These are bizzare and wonderful concepts, which even I don't fully understand hence will not talk in detail. Except for in layman terms, I can say that symmetry could be in many forms - reflectional ( you and yourself in mirror ), rotational ( square as seen fro axis ), translational ( this is tough one ! ) etc. Modular forms show inordinate level of symmetry, hence were intensely studied ( Penrose mad it even more famous ).


Taniyama and Shimura, two mathematicians from Japan, who were studying primarily modular forms, were able to link Elliptic Equations ( E series ) and the modular forms ( M series ) and proposed a conjecture popularly known as Taniyama-Shimura ( T-S ) conjecture. It stated that every elliptic equation is associated with a modular form. It was extraordinary and revolutionised the number theory. This was in line with the grand unification of mathematics as thought earlier, linking various mathematics. Modular Forms and Elliptic equations are two entirely different forms of mathematics, without linkages and here someone found one. So what does it do, if one is not able to solve a problem thru the elliptic equation route, he could pursue solution on modular route and convert it and vice-versa. This is like electricity and magnetism - two entirely different phenomena, linked by physicists ( one can produce electricity by magnetism and vice-versa ). Links are like Rosetta stone which helped us understand hieroglyphics by providing the right links between different languages.


Another mathematician attempted to link number theory and geometry and attempted to solve the FLT.


Meanwhile, Gerhard Frey, linked the elliptic equation and T-S conjecture with the proof of Fermat's Last Theorem. With deft maneovre's , he rearranged the equation

x^n + y^n = z^n ; to


y^2 = x^3 + ( A^N - B^N ) * x^2 - A^N * B^N, which is a elliptic equation.


He proved that this equation was 'weird' ( in mathematical terms ) and did not have a modular equivalent. But T-S conjecture said that every elliptical equation has a modular equivalent. The logic was built like this : If T-S conjecture is true - then every elliptic equation has a modular equivalent - so, then this eqn doesn't exist - if this doesn't exist, then there is no solution of Fermats Last Theorem - hence the theorem is 'true' or else T-S conjecture is 'false'. Hence if someone proved the T-S conjecture, he would have proved FLT.


Andrew Wiles worked on this and eventually proved the T-S conjecture, which led to the prove of FLT. He made this historic annoucement on June 23, 1993 at Newton Institute at Cambridge. As with any proof , its is rigorosly checked before being accepted. His proof was found to have some gaps, which is he worked on for a year and eventually plugged it.


He pursued his childhood dream, made it his passion. Hear it from the genius himself





What is still intriguing the mathematicians is that all this mathematics were invented in 20th century whereas Fermat wrote that he has a proof, in 17th century and that he did not have enough space in books margins... for sure it would have been based on 1th century mathematics...so what was the proof ? Go hunt it !!!